MR Ferry

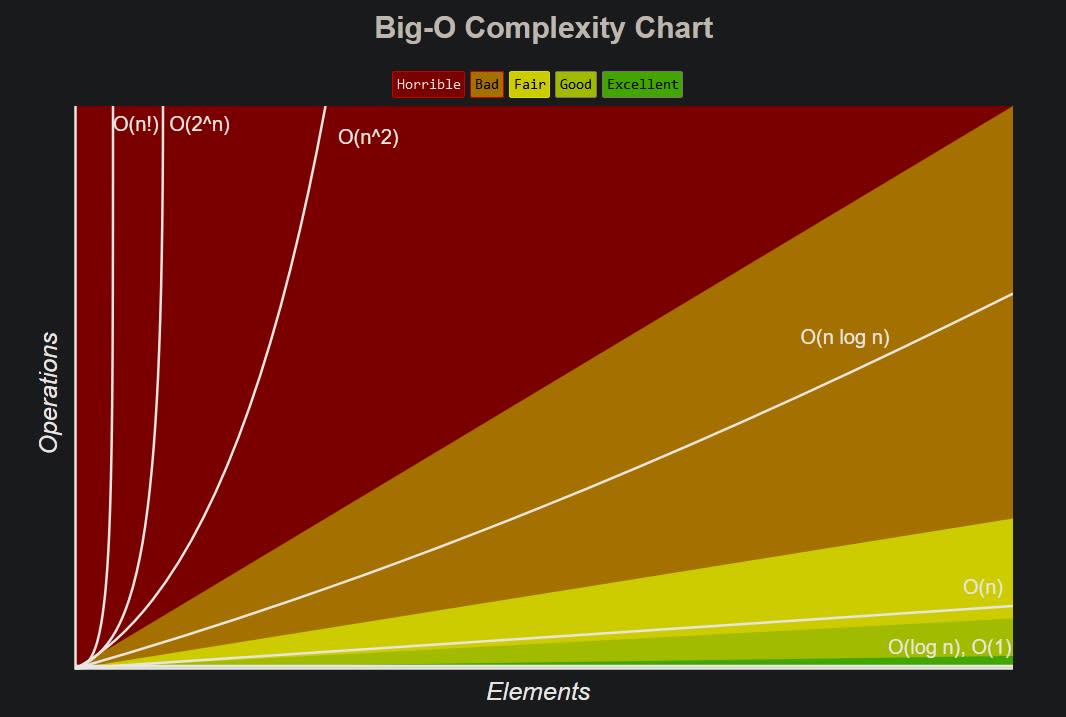
Big O Notation biasa digunakan untuk menghitung kompleksitas algoritma. Dalam pemrograman, ini sering dijadikan pedoman sebelum membuat keputusan pendekatan algoritma yang akan dipakai. Big O notation sendiri adalah tingkat kompleksitas operasi dari algoritma terhadap jumlah elemen yang diproses secara linear. Terdapat 2 jenis kompleksitas, yaitu space dan time. Yang akan gw bahas di sini hanyalah time complexity saja. Secara umum ada 8 jenis Big O notation.

O(1) Constant Time - Excellent👍

Ini jenis algoritma yang paling cepat, karena tidak peduli berapapun besar input yang diberikan, kecepatan prosesnya sama cepatnya karena hanya satu operasi yang dilakukan. Tidak perlu proses operasi yang berulang, tinggal eksekusi perintah langsung didapat hasilnya. Effort-nya hanya sekali proses.

Contoh O(1) di Dunia Nyata

Contohnya adalah saat melakukan pengecekan sebuah bilangan ganjil atau genap. Tinggal bagi 2 saja, kalau habis dibagi dua berarti genap, kalau nggak berarti ganjil. Ga perlu perulangan untuk mencari hasilnya. Contoh lainnya saat pengumuman undian door prize. Sebelum undian setiap peserta diberikan nomor unik dari 0-100. Ketika pengumuman tiba, MC tinggal teriak nyebutin nomor yang menang undian, misalnya "26". Maka otomatis orang yang punya nomor undian 26 maju ke depan. MC ga perlu nanyain peserta satu-persatu dari peserta nomor undian 0 hingga peserta nomor undian 100 untuk mengetahui siapa orangnya.

Contoh O(1) di Pemrograman

Mengambil nilai pada Array adalah contoh tipe data yang mengimplementasi O(1). Array cara kerjanya sama seperti analogi door prize di atas. Tinggal sebut mau index berapa langsung muncul nilainya. HashMap juga sama. Konsep kerja HashMap adalah dengan mengkalkulasi bitwise operation antara hashCode dari object yang dijadikan key dengan jumlah kapasitas HashMap yang hasilnya nanti dijadikan index untuk menyimpan object, makanya bisa O(1). Pembahasan lengkap mengenai Map & Collection udah gw tulis di artikel lain.

O(log(n)) Logarithmic - Good🙂

Nah, disini mungkin banyak yang bingung dengan logaritma. Logaritma sendiri adalah kebalikan dari bilangan berpangkat. Maksud log n pada Big O Notation adalah operasi tersebut umumnya dilakukan lebih dari satu kali dan tidak sebanyak jumlah input. Jadi O(log(n)) umumnya lebih cepat dari O(n) dan lebih lambat dari O(1).

Contoh O(log(n)) di Dunia Nyata

Misalkan kita ingin mencari terjemahan "god" dalam kamus bahasa Inggris. Hal yang pertama kita lakukan adalah membuka bagian tengah dari kamus tersebut. Ga efisien dong kalau kita buka kamus dari halaman depan karena kamus itu terurut dari A-Z. Hal yang selanjutnya kita lakukan adalah mengecek apakah hurufnya di sana diawali huruf "g" atau tidak. Misalnya hurufnya di sana diawali huruf "k", berarti kelewatan dong. Selanjutnya tentu kita balik beberapa halaman ke sebelah kiri, karena kalau balik ke halaman sebelah kanan makin kelewatan ntar😅. Misalnya hurufnya di sana diawali huruf "f", berarti missed juga, kita perlu balik sekian halaman lagi ke sebelah kanan. Kali ini hurufnya di sana diawali huruf "g", berarti udah deket, kita tinggal cek huruf kedua. Misalnya disana "goal", diawali dengan "go", berarti udah deket banget, tinggal cek di sekitar sana kata "god" dan selesai🤗. Di sini kita ga perlu cek semua kata satu-persatu dari halaman pertama seperti O(n).

Contoh O(log(n)) di Pemrograman

TreeMap (dan juga TreeSet) adalah contoh paling umum dan cara kerjanya mirip dengan mencari kata dalam kamus. TreeMap menyimpan key-nya secara terurut, jadi ketika ingin mencari key tertentu dia akan mencari dari root value (value pertama yang dimasukkan) dan mengecek apakah key yang dicari lebih besar atau lebih kecil dari root value. Jika lebih kecil dia akan mencari ke bagian key-key yang valuenya lebih kecil dari root dan mengabaikan key-key yang lebih besar dari root. Selanjutnya dia mengecek lagi dari sub root tersebut apakah lebih kecil atau lebih besar dari key yang dicari, persis seperti cara sebelumnya. Begitu seterusnya hingga key-nya equals.

O(n) Linear - Fair😐

Ini jenis algoritma yang penerapannya simple dan umum digunakan. Cara kerjanya adalah dengan melakukannya sebanyak n kali tergantung input.

Contoh O(n) di Dunia Nyata

Saat memindahkan 10 kulkas dari truk ke dalam rumah, yang kita lakukan adalah membawa satu kulkas dari truk ke dalam rumah, lalu kembali lagi ke truk dan bawa satu kulkas lagi ke rumah, lalu balik lagi dan seterusnya hingga 10 kali. Kita mengulangi prosesnya sebanyak jumlah kulkas yang ada.

Contoh O(n) di Pemrograman

Ketika membuat program yang melakukan print angka dari 1-10, sudah pasti kita akan melakukan print sebanyak 10 kali. Proses get() pada LinkedList juga O(n). LinkedList menerapkan konsep objek yang bertautan, dimana satu objek menyimpan objek sebelum dan sesudahnya. Jadi ketika kita ingin mengambil objek ke-10, maka behind the scene LinkedList mengambil objek 1 dan mengambil objek setelah objek 1 dan dari objek setelah objek 1 kita ambil lagi objek setelahnya, dan seterusnya hingga objek ke-10.

O(n * log(n)) Linearithmic - Bad☹️

Effortnya lebih besar dari O(n) tapi masih lebih baik dari O(n²). Biasanya terjadi ketika memproses masing-masing input tanpa harus membandingkannya dengan yang lain satu-persatu. Tidak seperti O(n²) yang memproses dan membandingkannya masing-masing satu-persatu.

Contoh O(n * log(n)) di Dunia Nyata

Contoh yang paling umum adalah menyusun puzzle gambar. Kita memilah potongan puzzle lalu mencocokkannya. Jika belum cocok kita akan menyimpan potongan tersebut pada tempat terpisah untuk dicocokkan kembali nanti. Lalu kita mengambil potongan lain untuk dicocokkan. Jika ada kesempatan maka kita akan mencocokkan potongan pertama tadi lagi, begitu seterusnya hingga semua puzzle tersusun sesuai semestinya. Di sini kita tidak perlu membandingkan masing-masing antara satu puzzle dengan puzzle lainnya seperti O(n²), melainkan memisahkan antara yang sudah pernah dicocokkan dengan yang belum. Dan yang belum nantinya akan dicocokkan lagi ketika ada kesempatan.

Contoh O(n * log(n)) di Pemrograman

Umumnya, algoritma sorting pada bahasa pemrograman menggunakan metode Merge Sort seperti pada Javascript atau Collections.sort() pada Java. Yaitu dengan memecah elemen menjadi beberapa bagian yang kecil lalu bagian-bagian kecil tersebut diurutkan dan digabungkan kembali dengan bagian kecil lainnya hingga semuanya terurut. Pada Java, Arrays.sort() menggunakan Quick Sort yang juga memiliki kompleksitas rata-rata O(n * log(n)). Karena kompleksitas O(n * log(n)) inilah makanya untuk memproses elemen yang terurut dianjurkan untuk menggunakan TreeMap atau TreeSet daripada menyimpan nilai pada Array atau Collection lalu sorting. Kecuali ada requirement khusus.

O(n²) Quadratic - Horrible😡

O(n²) alias O(n * n) berarti effort yang dibutuhkan lebih besar dua kali lipat daripada O(n). Semakin besar total input, semakin lebih besar lagi effort yang dibutuhkan hingga dua kali lipat. Misalnya jika total inputnya 2 maka total operasinya nanti 4, jika total inputnya 6 maka total operasinya 36, dan seterusnya.

Contoh O(n²) di Dunia Nyata

Pada saat menghitung beberapa barang yang dibeli dari beberapa toko. Pada toko sepatu kita membeli beberapa sepatu, pada toko baju kita membeli beberapa baju, pada toko celana kita membeli beberapa celana. Untuk menghitung jumlahnya pasti kita akan menghitung berapa item yang kita beli masing-masing di toko sepatu, toko baju dan toko celana. Semakin banyak toko dan item yang dibeli, semakin lama lagi proses menghitungnya.

Contoh O(n²) di Pemrograman

Program yang membutuhkan perulangan bersarang (nested loop) memiliki kompleksitas O(n²). Membuat program untuk mengecek jumlah toko dan barang seperti kasus di atas salah satu contohnya, karena kita melakukan penghitungan jumlah tokonya dan jumlah item masing-masing toko. Melakukan sorting dengan metode bubble sort juga sama, karena kita membandingkan nilai pertama dengan nilai kedua hingga nilai terakhir. Lanjut membandingkan nilai kedua dengan nilai ketiga hingga nilai terakhir. Dan seterusnya hingga terurut.

O(2ⁿ) Exponential - Horrible😡

Effort operasinya bertambah 2 kali lebih besar setiap pertambahan total input. Untuk lebih jelasnya liat contohnya aja, gw juga bingung mendefinisikannya😂.

Contoh O(2ⁿ) di Dunia Nyata

Pada saat membeli mie di warung, biasanya kita bisa request dengan 3 opsi, goreng atau rebus, dibungkus atau makan di tempat, pake telur atau tanpa telur. Nah, total semua kombinasi itu kompleksitasnya O(2ⁿ). Dimana kita bisa mendapatkan kombinasi:

• mie goreng, dibungkus, pake telur;
• mie goreng, dibungkus, tanpa telur;
• mie goreng, makan di tempat, pake telur;
• mie goreng, makan di tempat, tanpa telur;
• mie rebus, dibungkus, pake telur;
• mie rebus, dibungkus, tanpa telur;
• mie rebus, makan di tempat, pake telur;
• mie rebus, makan di tempat, tanpa telur;

Contoh O(2ⁿ) di Pemrograman

Contohnya saat mencari subset dari sebuah array. Misalnya terdapat array {1,2,3} dan kita ingin mencari subset array yang dihasilkan dari array tersebut. Pertama tentu saja adalah array kosong, {}. Selanjutnya, kita mengambil subset 1 bilangan, mulai dari {1}, {2} dan {3}. Lalu subset 2 bilangan, mulai dari {1,2}, {1,3}, dan {2,3}. Terakhir subset 3 bilangan, yaitu {1,2,3}. Jadi, totalnya ada 8 subset dari array {1,2,3}.

O(n³) Cubic - Horrible😡

Tentu saja ini lebih kompleks lagi dari O(n²). Sebenarnya secara definisi mirip seperti O(n²) tapi dua kali lebih kompleks lagi dari O(n²).

Contoh O(n³) di Dunia Nyata

Di Excel ada sheet, row dan cell. Ketika ingin mengecek nilai dari masing-masing cell pasti kita akan mengeceknya dari sheet pertama dan row pertama. Lanjut ke cells pada sheet pertama dan row kedua. Hingga seterusnya. Setelah selesai sheet pertama, lanjut cells pada sheet kedua dan row pertama. Lalu cells pada sheet kedua dan row kedua. Hingga seterusnya sampai selesai.

Contoh O(n³) di Pemrograman

Ga usah jauh-jauh, ketika membuat program laporan dengan memproses sheet, row dan cell pada excel seperti kasus di atas sudah pasti menggunakan kompleksitas O(n³).

O(n!) Factorial - Ultra Horrible🤬

Algoritma paling parah dibanding lainnya. Semakin besar input, semakin lebih besar lagi prosesnya bahkan berkali-kali lipat.

Contoh O(n!) di Dunia Nyata

Misalkan sebuah koper memiliki password angka 3 buah digit. Untuk mengetahui password dari koper tersebut kita bisa melakukan brute force. Kita mencoba segala bentuk permutasinya. Mulai dari {1,2,3}, {3,2,1}, {2,1,3}, {1,3,2}, {2,3,1}, dan lainnya. Dalam dunia hacker, ini adalah cara paling pasrah seorang hacker yang sudah kehabisan akal untuk melakukan hacking🤣.

Contoh O(n!) di Pemrograman

Algoritma ini paling jarang dipraktekkan dan cenderung dihindari karena kompleksitasnya sangat buruk. Kasus seperti ini biasanya ditemui saat tes pemrograman online. Seperti mencari permutasi bilangan.

Catatan Tambahan

Oh ya, kadang ada juga yang salah kaprah mengenai O(n). Contohnya ketika melakukan loop yang sama lebih dari satu kali seperti ini:

let x = 10;
let arr1 = [];
for(let i = 0; i < x; i++){
	arr1.push(i);
}
let arr2 = [];
for(let i = 0; i < x; i++){
	arr2.push(i);
}

Ada yang beranggapan itu adalah O(2n) atau O(n + n) sehingga lebih buruk dibanding digabung. Padahal bukan, Big O Notation itu hitungan kompleksitas terhadap argument secara linear. Code tersebut ga ada bedanya secara kompleksitas dengan code berikut:

let x = 10;
let arr1 = [];
let arr2 = [];
for(let i = 0; i < x; i++){
	arr1.push(i);
	arr2.push(i);
}

Kedua code di atas sama-sama O(n) karena sama-sama linear. Keduanya sama-sama melakukan push arr1 dan arr2 masing-masing sebanyak 10 kali. Memecah code menjadi 2 buah loop yang sama tidak membuat kompleksitas jadi lebih buruk. Justru itu menjadikan code Single Responsibility. Contohnya seseorang yang ditugaskan memakan 10 buah mangga dan 10 buah apel. Dia bisa saja memakan buah mangga terlebih dahulu satu-persatu sampai habis, lalu dilanjutkan memakan buah apel satu-persatu sampai habis seperti code pertama. Atau bisa juga dengan cara memakan satu buah mangga, lalu lanjut makan satu buah apel, dilakukan secara bergantian satu-persatu hingga kedua buah tersebut habis seperti code kedua. Effort keduanya sama-sama memakan buah sebanyak 20 buah. "n" itu bukan jumlah looping, tapi jumlah input operasionalnya, yaitu sama-sama 20 kali dalam hal ini.

Kesimpulan

Itulah 8 Big O Notation yang umum dijadikan pertimbangan ketika mengimplementasi sebuah code agar algoritma yang dibuat optimal dan efisien. Performance adalah salah satu bagian penting pada sebuah program. Apalagi bagi user jaman sekarang, ada aplikasi yang lemot dikit aja bisa bisa pindah ke kompetitor😅.